Numbering Systems (Second of Four Parts: Binary)
Numbering system based on 2
- 2 symbols: 0, 1
- Powers of 2
Data communication systems and computers use binary numbers to represent control information and data. The binary number system is exactly the same as the decimal number system, except it is based on two instead of ten. You could even call it base 2 arithmetic if you wanted to.
There are two symbols in the binary number system: 0 and 1. Quantities are represented as powers of two.
When expressing quantities in the binary number system, we use a shorthand notation to indicate how many of which powers of ten are needed to make up the quantity.
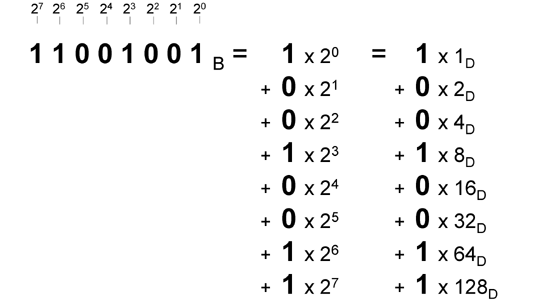
For example, when we write the number “11001001”, what we mean is
1 x 27 + 1 x 26 + 0 x 25 + 0 x 24 + 1 x 23 + 0 x 22 + 0 x 21 + 1 x 20 .
This could also be written as
(1 x 27) + (1 x 26) + (0 x 25) + (0 x 24) + (1 x 23 ) + (0 x 22) + (0 x 21) + (1 x 0 ) .
The binary digits 1, 1, 0, 0, 1, 0, 0 and 1 indicate, for the appropriate power of 2, how many of that power of two go in to making up the quantity. In other words, the numbers 1, 1, 0, 0, 1, 0, 0 and 1 are placeholders in our shorthand notation, indicating how many of the powers of two in that place go in to making up the quantity.
Compare this to our understanding of decimal numbers, and you will see that the concept of binary and decimal are the same - only the base is different. Decimal is based on ten and binary is based on two.









